[Machine Learning] 의사결정 트리(Decision Tree) 알고리즘으로 서울 지역 다중 분류하기!
오늘 소개할 알고리즘은 의사결정 트리(Decision Tree) 알고리즘이다.
이 알고리즘과 서울 지역의 위도, 경도 Data를 활용하여 서울 지역을 강북, 강남, 강동, 강서 총 4개의 지역으로 다중 분류하는 예제를 실습해보았다!
의사결정 트리 알고리즘은 Data 분류(Classification)와 회귀(Regression)에 사용되는 지도학습(Supervised Learning) 알고리즘이다.
의사결정 트리 알고리즘에 대한 내 나름의 설명을 해보도록 하겠다!
이론
Data의 특징을 바탕으로 한 질문들을 통해 Data를 연속적으로 분리하는 과정을 거쳐 하나의 값으로 Data를 분류하는 알고리즘
아무 질문이 아닌, Data들의 특징 중 Data를 분류하는데 큰 영향을 끼치는 특징들을 우선적으로 질문하면서(상위 노드로 선택) Data를 최종적으로 분류해내는 것임.(스무고개와 굉장히 유사!)
상위 노드에는 영향력이 큰 특징을, 하위 노드에는 영향력이 작은 특징을 위치시킨다. 결국 이렇게 ‘영향력이 작고 크다‘라는 것을 판단하려면 수치적인 결과가 필요하다. 그래서 사용하는 것이 ‘정보 이론(Information Theory)‘의 ‘엔트로피(Entropy)’ 개념이다!
사용되는 용어/개념 정리
의사결정 트리 알고리즘에서 사용되는 용어와 개념들에 대해서 간단히 알아보도록 하자!
* 엔트로피(Entropy)
엔트로피(Entropy)란,
정답에 대한 불확실성을 수치적으로 표현한 값
정보 이론(Information Theory)에서는 ‘질문을 할 때마다 정보를 약간씩 얻는 과정’이 ‘정답에 대한 불확실성을 점점 줄여나가는 것’과 동일한 개념으로 본다. 이때 이 불확실성을 ‘엔트로피’라고 표현하는 것이다.
* 정보이득(Information gain)
정보 이득(Information gain)이란,
질문 전의 엔트로피 값 - 질문 후의 엔트로피 값
즉, 질문을 함으로써 줄어들게된 불확실성의 값을 나타낸다.
확률에 기반한 정보 엔트로피
엔트로피를 구하는 공식은 다음과 같다.
Entropy = $\sum_{i=1}^m -p_i \log_2 pi$
- $p_i$ : Data 중 범주 i에 속하는 Data의 비율(확률)
특징에 대한 엔트로피 계산
하나의 특징을 통해 Data를 한 번 분리했을 때의 엔트로피를 구하는 공식은 다음과 같다.
Entropy = $\sum_{c \in X} P(c)E(c)$
- $X$ : 선택한 특징
- $c$ : 선택한 특징에 의해 생성되는 하위 노드
- $P(c)$ : 선택한 특징에 의해 생성된 하위 노드에 Data가 속할 확률
- $E(c)$ : 선택한 특징에 의해 생성된 하위 노드의 엔트로피
이렇게 각 특징에 대한 엔트로피를 계산했을 때 그 엔트로피의 값이 가장 작은 값 즉, 불확실성이 가장 적은 노드를 상위 노드로 선택하는 것이 효율적인 의사결정 트리를 구성할 수 있다!
* 지니 계수(Gini coefficient)
지니 계수(Gini coefficient)란,
CART 타입의 의사결정 트리에서 사용하는 것으로써, 분류된 집합에 이질적인 Data가 얼마나 섞여있는지를 측정할 수 있는 지표
‘CART’란 ‘Classification And Regression Tree’의 약자. ‘CART’는 각 노드마다의 특징을 이진으로 분류하는 특징을 가지고 있다. 그리고 이 과정에서 노드의 상하위 위치를 고려할 때 지니 계수를 사용한다.
지니 계수가 높을수록 순도가 높다.
- 순도가 높다 = 한 그룹에 모여있는 Data들의 속성들이 많이 일치하고 있다.
- 불순도가 높다(순도가 낮다) = 한 그룹에 여러 속성을 가진 Data들이 많이 섞여 있다.
즉, 지니 계수가 높은(순도가 높은) 특징들을 상위 노드에 위치하는 것이 좋다!
그럼 특징에 대한 지니 계수는 어떻게 구하는가?
- 한 가지의 특징으로 분리된 두 노드의 지니 계수를 각각 구함. => $P^2 + Q^2$
- $P$, $Q$ : 해당 노드로 분리되는 Data의 비율
- 특징에 대한 지니 계수를 구함.(두 노드의 지니 계수를 더하면 됨)
장/단점
장점
- 이 결과값이 왜 나왔는지, 어떻게 나왔는지 이해하기 쉬움.
- 수치 Data 뿐만 아니라 범주 Data에도 적용이 가능한 알고리즘.
단점
- 과대적합(Overfitting)의 위험이 높다.
예제) 서울 지역(강동, 강서, 강남, 강북) 다중 분류하기
Data 준비
import pandas as pd
district_dict_list = [
{'district': 'Gangseo-gu', 'latitude': 37.551000, 'longitude': 126.849500, 'label':'Gangseo'},
{'district': 'Yangcheon-gu', 'latitude': 37.52424, 'longitude': 126.855396, 'label':'Gangseo'},
{'district': 'Guro-gu', 'latitude': 37.4954, 'longitude': 126.8874, 'label':'Gangseo'},
{'district': 'Geumcheon-gu', 'latitude': 37.4519, 'longitude': 126.9020, 'label':'Gangseo'},
{'district': 'Mapo-gu', 'latitude': 37.560229, 'longitude': 126.908728, 'label':'Gangseo'},
{'district': 'Gwanak-gu', 'latitude': 37.487517, 'longitude': 126.915065, 'label':'Gangnam'},
{'district': 'Dongjak-gu', 'latitude': 37.5124, 'longitude': 126.9393, 'label':'Gangnam'},
{'district': 'Seocho-gu', 'latitude': 37.4837, 'longitude': 127.0324, 'label':'Gangnam'},
{'district': 'Gangnam-gu', 'latitude': 37.5172, 'longitude': 127.0473, 'label':'Gangnam'},
{'district': 'Songpa-gu', 'latitude': 37.503510, 'longitude': 127.117898, 'label':'Gangnam'},
{'district': 'Yongsan-gu', 'latitude': 37.532561, 'longitude': 127.008605, 'label':'Gangbuk'},
{'district': 'Jongro-gu', 'latitude': 37.5730, 'longitude': 126.9794, 'label':'Gangbuk'},
{'district': 'Seongbuk-gu', 'latitude': 37.603979, 'longitude': 127.056344, 'label':'Gangbuk'},
{'district': 'Nowon-gu', 'latitude': 37.6542, 'longitude': 127.0568, 'label':'Gangbuk'},
{'district': 'Dobong-gu', 'latitude': 37.6688, 'longitude': 127.0471, 'label':'Gangbuk'},
{'district': 'Seongdong-gu', 'latitude': 37.557340, 'longitude': 127.041667, 'label':'Gangdong'},
{'district': 'Dongdaemun-gu', 'latitude': 37.575759, 'longitude': 127.025288, 'label':'Gangdong'},
{'district': 'Gwangjin-gu', 'latitude': 37.557562, 'longitude': 127.083467, 'label':'Gangdong'},
{'district': 'Gangdong-gu', 'latitude': 37.554194, 'longitude': 127.151405, 'label':'Gangdong'},
{'district': 'Jungrang-gu', 'latitude': 37.593684, 'longitude': 127.090384, 'label':'Gangdong'}
]
train_df = pd.DataFrame(district_dict_list)
train_df = train_df[['district', 'longitude', 'latitude', 'label']]
# Test할 때 사용할 동 정보 Data
dong_dict_list = [
{'dong': 'Gaebong-dong', 'latitude': 37.489853, 'longitude': 126.854547, 'label':'Gangseo'},
{'dong': 'Gochuk-dong', 'latitude': 37.501394, 'longitude': 126.859245, 'label':'Gangseo'},
{'dong': 'Hwagok-dong', 'latitude': 37.537759, 'longitude': 126.847951, 'label':'Gangseo'},
{'dong': 'Banghwa-dong', 'latitude': 37.575817, 'longitude': 126.815719, 'label':'Gangseo'},
{'dong': 'Sangam-dong', 'latitude': 37.577039, 'longitude': 126.891620, 'label':'Gangseo'},
{'dong': 'Nonhyun-dong', 'latitude': 37.508838, 'longitude': 127.030720, 'label':'Gangnam'},
{'dong': 'Daechi-dong', 'latitude': 37.501163, 'longitude': 127.057193, 'label':'Gangnam'},
{'dong': 'Seocho-dong', 'latitude': 37.486401, 'longitude': 127.018281, 'label':'Gangnam'},
{'dong': 'Bangbae-dong', 'latitude': 37.483279, 'longitude': 126.988194, 'label':'Gangnam'},
{'dong': 'Dogok-dong', 'latitude': 37.492896, 'longitude': 127.043159, 'label':'Gangnam'},
{'dong': 'Pyoungchang-dong', 'latitude': 37.612129, 'longitude': 126.975724, 'label':'Gangbuk'},
{'dong': 'Sungbuk-dong', 'latitude': 37.597916, 'longitude': 126.998067, 'label':'Gangbuk'},
{'dong': 'Ssangmoon-dong', 'latitude': 37.648094, 'longitude': 127.030421, 'label':'Gangbuk'},
{'dong': 'Ui-dong', 'latitude': 37.648446, 'longitude': 127.011396, 'label':'Gangbuk'},
{'dong': 'Samcheong-dong', 'latitude': 37.591109, 'longitude': 126.980488, 'label':'Gangbuk'},
{'dong': 'Hwayang-dong', 'latitude': 37.544234, 'longitude': 127.071648, 'label':'Gangdong'},
{'dong': 'Gui-dong', 'latitude': 37.543757, 'longitude': 127.086803, 'label':'Gangdong'},
{'dong': 'Neung-dong', 'latitude': 37.553102, 'longitude': 127.080248, 'label':'Gangdong'},
{'dong': 'Amsa-dong', 'latitude': 37.552370, 'longitude': 127.127124, 'label':'Gangdong'},
{'dong': 'Chunho-dong', 'latitude': 37.547436, 'longitude': 127.137382, 'label':'Gangdong'}
]
test_df = pd.DataFrame(dong_dict_list)
test_df = test_df[['dong', 'longitude', 'latitude', 'label']]
이번 실습 예제에서 사용할 Data들을 Pandas의 DataFrame 형태로 변수에 저장하였다.
이 Data의 Index에 대한 설명은 다음과 같다.
Data에 대한 설명
- district : 행정 구역(서초구, 송파구 등)
- dong : 동(대치동, 서초동 등)
- latitude : 위도, longitude : 경도
- label : 한강 기준으로 동, 서, 남, 북으로 구분한 명칭(강동, 강서, 강남, 강북)
value_counts()함수를 통해서 학습 Data와 테스트 Data의 label 정보를 확인해보면 다음과 같다.
train_df.label.value_counts()
Gangseo 5
Gangdong 5
Gangbuk 5
Gangnam 5
Name: label, dtype: int64
test_df.label.value_counts()
Gangseo 5
Gangdong 5
Gangbuk 5
Gangnam 5
Name: label, dtype: int64
위도와 경도 정보를 가지고 학습 Data의 위치 정보를 시각화해보면 다음과 같다.
2차원 평면의 그래프로 나타내기 위해 matplotlib와 seaborn 모듈을 이용하였다.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.lmplot('longitude', 'latitude', data = train_df, fit_reg = False,
scatter_kws = {'s':150}, # 좌표 상의 점 크기
markers = ['o', 'x', '+', '*'],
hue = 'label') # 예측값
plt.title("District visualization in 2d plane")
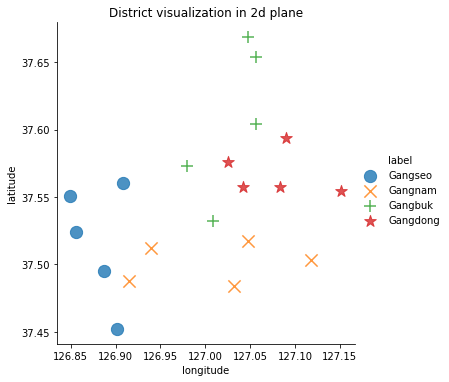
Data 전처리
학습 및 테스트에 필요 없는 특징(Column)들을 Data에서 제거하는 전처리 과정(Preprocessing)을 진행했다.
학습 및 테스트에 구, 동 이름은 필요하지 않기 때문에 drop()함수를 이용하여 제거했다.
train_df.drop(['district'], axis = 1, inplace = True)
test_df.drop(['dong'], axis = 1, inplace = True)
X_train = train_df[['longitude', 'latitude']]
y_train = train_df[['label']]
X_test = test_df[['longitude', 'latitude']]
y_test = test_df[['label']]
모델 학습
사이킷런(scikit-learn)의 의사결정 트리 모드를 이용하여 의사결정 트리 모델을 학습하였다.
코드는 다음과 같다.
from sklearn import tree, preprocessing
import numpy as np
import matplotlib.pyplot as plt
le = preprocessing.LabelEncoder()
y_encoded = le.fit_transform(y_train)
# 'le.classes_' -> Mapping된 인덱스 확인할 수 있음!
clf = tree.DecisionTreeClassifier(random_state = 35).fit(X_train, y_encoded)
# 의사결정 트리 객체를 생성 후, 바로 학습 Data를 fit함.
# 'random_state'는 랜덤한 값을 고정시키는 시드같은 개념!
# 숫자를 지정함으로써 동일하게 랜덤한 값을 생성시킬 수 있도록 하는 것
의사결정 트리 모델의 결정 경계 시각화
위에서 학습한 의사결정 트리 모델의 결정 경계가 어떻게 보여지는지 시각화하는 코드이다.
코드를 함수로 정의해서 사용하기 편리하도록 하였다.
def display_decision_surface(clf, X, y):
x_min = X.longitude.min() - 0.01
x_max = X.longitude.max() + 0.01
y_min = X.latitude.min() - 0.01
y_max = X.latitude.max() + 0.01
# 그래프의 x, y축을 시각적으로 더 좋게 보이게하기 위해 축 값을 조정
n_classes = len(le.classes_) # '강북, 강남, 강동, 강서' 총 4개
plot_colors = 'rywb' # 점 색깔
plot_step = 0.001 # 축 간격
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
np.arange(y_min, y_max, plot_step))
# 직사각형 Grid(격자) 생성
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap = plt.cm.RdYlBu)
for i, color in zip(range(n_classes), plot_colors):
idx = np.where(y == i) # 조건을 만족하는 값의 index를 'idx' 변수에 저장
plt.scatter(X.loc[idx].longitude, X.loc[idx].latitude,
c = color, label = le.classes_[i],
cmap = plt.cm.RdYlBu, edgecolor = 'black', s = 200)
plt.title("Decision surface of a decision tree", fontsize = 16)
plt.legend(bbox_to_anchor = (1.05, 1), loc = 2, borderaxespad = 0, fontsize = 14)
plt.xlabel('longitude', fontsize = 16)
plt.ylabel('latitude', fontsize = 16)
plt.rcParams['figure.figsize'] = [7, 5] # 그래프 크기
plt.rcParams['font.size'] = 14
plt.rcParams['xtick.labelsize'] = 14 # x축 글씨 크기
plt.rcParams['ytick.labelsize'] = 14 # y축 글씨 크기
plt.show()
display_decision_surface(clf, X_train, y_encoded)
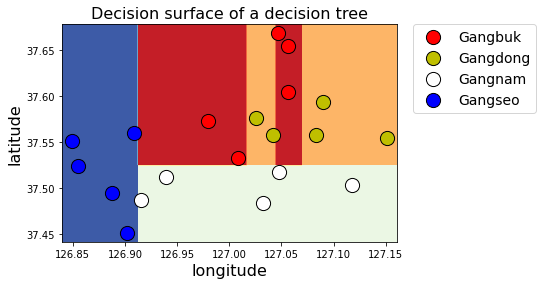
위의 그래프를 살펴보자!
그래프에서 ‘강북(빨간색)’과 ‘강동(노란색)’에 해당하는 Data를 보게 되면, 지나치게 학습 Data에 의존하여 학습했다고 볼 수 있다. 즉, 과대적합(Overfitting)이 된 것이다.
실제 저 지역은 저렇게 경계가 나눠지지 않는다.
따라서 처음에 DecisionTreeClassifier() 객체를 만들 때, 별도의 Parameter들을 추가적으로 지정함으로써 과대적합을 줄일 수 있다.
clf = tree.DecisionTreeClassifier(max_depth = 4,
min_samples_split = 2,
min_samples_leaf = 2,
random_state = 70).fit(X_train, y_encoded)
display_decision_surface(clf, X_train, y_encoded)
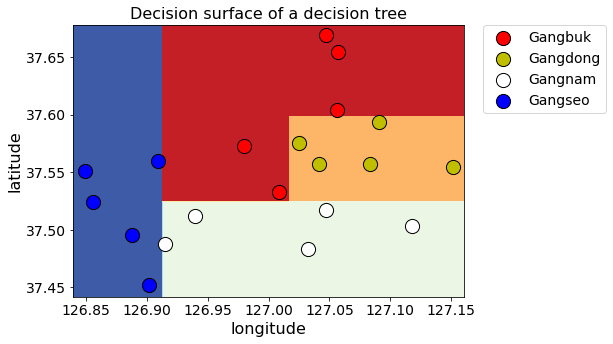
모델에 사용한 Parameter 설명
- max_depth : Tree의 최대 한도 깊이
- min_samples_split : 자식 노드를 갖기 위한 최소한의 Data 개수
- min_samples_leaf : 리프 노드(최하위의 노드)의 최소 Data 개수
- random_state : 동일한 정수를 입력하면 학습 결과를 항상 같게 만들어주는 파라미터
Parameter를 사용해서 모델을 학습한 결과와 사용하지 않은 결과를 비교해보자.
Parameter를 사용했을 때가 아닌 모델보다 서울 지역을 분류하려는 예제의 목표에 더 적합하다는 것을 확인할 수 있다.
모델 테스트
위에서 학습된 모델에 테스트 Data를 가지고 예측값과 실제값을 비교해보았다.
from sklearn.metrics import accuracy_score
pred = clf.predict(X_test)
print('accuracy : {}'.format(accuracy_score(y_test.values.ravel(), le.classes_[pred])))
accuracy : 1.0
정확도가 1.0(100%)인 것을 확인할 수 있다.
결과를 표(DataFrame)로 확인하면 다음과 같다.
comparison = pd.DataFrame({"prediction":le.classes_[pred],
"ground_truth":y_test.values.ravel()})
comparison
| prediction | ground_truth | |
|---|---|---|
| 0 | Gangseo | Gangseo |
| 1 | Gangseo | Gangseo |
| 2 | Gangseo | Gangseo |
| 3 | Gangseo | Gangseo |
| 4 | Gangseo | Gangseo |
| 5 | Gangnam | Gangnam |
| 6 | Gangnam | Gangnam |
| 7 | Gangnam | Gangnam |
| 8 | Gangnam | Gangnam |
| 9 | Gangnam | Gangnam |
| 10 | Gangbuk | Gangbuk |
| 11 | Gangbuk | Gangbuk |
| 12 | Gangbuk | Gangbuk |
| 13 | Gangbuk | Gangbuk |
| 14 | Gangbuk | Gangbuk |
| 15 | Gangdong | Gangdong |
| 16 | Gangdong | Gangdong |
| 17 | Gangdong | Gangdong |
| 18 | Gangdong | Gangdong |
| 19 | Gangdong | Gangdong |

댓글남기기