[Machine Learning] 앙상블(Ensemble) 기법을 활용해 손글씨 분류하기!

오늘 소개할 알고리즘은 앙상블(Ensemble) 기법이다.

앙상블 기법은 여러 개의 모델을 조합해서 더 나은 성능을 내도록 하는 기법이다!

이번에 앙상블 기법을 이용한 예제에서는 그동안 알아보았던 ‘k-NN’, ‘SVM’, ‘Decision Tree’ 알고리즘과 손글씨 데이터셋을 이용하여 손글씨 분류를 해보았다.

일단 앙상블 기법에 대해서 설명해보도록 하겠다.

　

　

이론

여러 개의 분류 모델을 조합해서 더 나은 성능을 내는 방법

앙상블(Ensemble) 기법에는 크게 배깅(Bagging), 부스팅(Boosting) 이렇게 2가지 방식이 있다.

　

배깅(Bagging)

한 종류의 분류 모델을 여러 개 만든 후, 서로 다른 학습 Data로 학습시키고 동일한 테스트 Data에 대한 예측값들을 투표해서 가장 높은 예측값으로 결론내리는 기법

배깅(Bagging)은 부트스트랩(Bootstrap)과 어그리게이팅(Aggregating)의 줄임말이다.

배깅은 과대적합(Overfitting)이 쉬운 모델에 굉장히 적합한 앙상블 기법이다. 대표적으로 과대적합이 쉬운 ‘의사결정 트리(Decision Tree)’모델에 많이 사용된다.

　

부트스트랩(Bootstrap)

Data를 일부러 편향되도록 Sampling하는 기법

과대적합 모델은 학습 Data에 대해서는 높은 정확도를 보여주지만, 그 외의 새로운 Data에 대해서는 낮은 정확도를 보여준다.

부트스트랩(Bootstrap) 기법을 통해서 Data를 Sampling할 때, 편향(bias)을 높여서 과대적합 위험성을 줄이는 것이다.

부트스트랩은 n개의 Data를 k개의 학습 Data로 나눌 때, 중복을 허용해서 편향을 높이는 방식을 사용한다.

일반적으로 Data의 총 개수인 n개보다 적은 개수의 Data를 할당하게 된다.(일반적으로 전체 Data의 6~70%정도)

예를 들면,

• 전체 Data : [1, 2, 3, 4, 5]

일 때 5개의 학습 Data를 부트스트랩 기법을 사용해서 나누면,

• 학습 Data 1 : [1, 3, 4]
• 학습 Data 2 : [1, 2, 5]
• 학습 Data 3 : [3, 5, 4]
• 학습 Data 4 : [2, 4, 1]
• 학습 Data 5 : [1, 4, 5]

이렇게 중복을 허용해서 나누게 되는 것이다.

　

어그리게이팅(Aggregating)

여러 분류 모델이 예측한 값을 ‘투표’를 통해서 하나의 결론으로 도달하는 과정

　

하드 보팅(Hard Voting)

여러 개의 분류 모델에서 나온 결과 중 가장 많이 나온 예측값을 선정하는 것

만약 숫자를 1 ~ 5로 분류하는 의사결정 트리 5개를 학습했다고 하자. 이때 5개의 결과 중 가장 많이 나온 결과로 예측값을 선정하는 것이다.

　

소프트 보팅(Soft Voting)

각 분류값의 확률을 더한 값을 점수로 사용해서 가장 높은 점수를 가지는 분류값을 선정하는 것

k개의 모델이 각 레이블로 분류할 확률을 레이블 별로 합산해서 제일 높은 점수를 가지는 것으로 예측값(레이블)을 선정하는 것이다.

　

랜덤 포레스트(Random Forest)

여러 개의 의사결정 트리를 배깅해서 예측을 실행하는 모델

의사결정 트리(나무)를 여러개 모아놓았다고 해서 ‘랜덤 포레스트(Random Forest)’라는 이름이 붙여졌다.

의사결정 트리 기법에서 배깅을 사용한 대표적인 알고리즘이다.

　

　

부스팅(Boosting)

동일한 알고리즘의 분류기를 순차적으로 학습해서 여러 개의 분류기를 만든 후, 테스트 단계에서 가중 투표를 통해 예측값을 결정하는 기법

배깅(Bagging)은 여러 분류기 모델을 병렬적으로 학습시켜서 예측값을 얻어내는 기법이라면,

부스팅(Boosting)은 동일한 분류기를 순차적으로 학습시켜서 여러 개의 분류기 모델을 만들고, 가중 투표를 통해 예측값을 얻어내는 기법이다.

　

순차적 학습

말 그대로 ‘순차적으로’ 학습하는 과정을 의미한다.

먼저 첫 번째 분류기를 학습하게 된다. 만약 첫 번째 학습에서 미흡한 부분이 발견되면, 그 부분에 대한 학습 Data를 보강해서 다시 학습시켜 두 번째 분류기를 만든다.

그리고 두 번째 학습의 테스트 결과에 따라서 또 미흡한 부분의 학습 Data를 보강하여 다시 학습을 시켜 세 번째 분류기를 만든다.

이러한 과정을 반복함으로써 여러 개의 분류기를 만들게 되는 것이다.

이 과정을 통해서 부스팅 기법은 동일한 알고리즘을 가지는 여러 개의 분류기를 만들게 되는 것이다.

　

가중 투표

더 많은 학습을 거친 분류기에 따라서 높은 가중치를 부여해서 분류값을 선정하는 것

가중 투표에도 하드 보팅(Hard Voting)과 소프트 보팅(Soft Voting) 2가지가 있다. 이는 위에서 설명한 하드 보팅, 소프트 보팅과 동일하다. 다만 가중치가 부여될 뿐.

예시를 통해서 알아보도록 하겠다.

예를 들어, 사진을 보고 남자인지 여자인지 분류하는 분류기가 있다고 가정하자

각 분류기가 보여주는 정확도와 분류값이 다음과 같다.

	분류기1	분류기2	분류기3
정확도	0.4	0.5	0.95
분류값	남자	남자	여자

먼저 하드 보팅의 경우 가중 투표를 진행하면 다음과 같다.

• 남자 = 0.4 + 0.5
• 여자 = 0.95

따라서 분류기 2개가 남자로 분류했음에도 불구하고 최종적인 분류값은 여자로 분류하게 된다.

소프트 보팅의 경우 가중 투표를 진행하면 다음과 같다.

	분류기1	분류기2	분류기3
분류값	남자:0.7 / 여자:0.3	남자:0.8 / 여자:0.2	남자:0.1 / 여자:0.9

• 남자 = 0.4x0.7 + 0.5x0.8 + 0.95x0.1 = 0.775
• 여자 = 0.4x0.3 + 0.5x0.2 + 0.95x0.9 = 1.075

즉, (분류기의 정확도) x (분류값으로 분류할 확률)을 각 레이블 별로 모두 더하는 것이다.

　

　

예제1) 랜덤 포레스트 손글씨 분류

손글씨 분류를 위한 데이터셋으로 ‘MNIST 손글씨 데이터셋’을 이용하였다.

# 사용할 모듈 Import하기

from sklearn import datasets
from sklearn import tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

　

Data 불러오기

mnist = datasets.load_digits()
features = mnist.data
labels = mnist.target

　

　

교차 검증

MNIST 손글씨 데이터셋에 대해서 각 모델의 정확도를 알아보기 위해서 교차 검증을 진행하는 함수를 다음과 같이 정의하였다.

교차 검증을 10번 수행해서 정확도를 평균을 내는 과정을 10번 반복하도록 함수를 정의한 것이다.

def cross_validation(classifier, features, labels):
    cv_scores = []
    for i in range(10):  # 교차 검증 10번 수행
        scores = cross_val_score(classifier, features, labels, 
                                cv = 10, scoring = 'accuracy')
        cv_scores.append(scores.mean())
    return cv_scores

# 의사결정 트리(Decision Tree) 정확도

dt_cv_scores = cross_validation(tree.DecisionTreeClassifier(),
                               features, labels)

# 랜덤 포레스트(Random Forest) 정확도

rf_cv_scores = cross_validation(RandomForestClassifier(),
                               features, labels)

　

　

랜덤 포레트스 vs 의사결정 트리의 정확도 시각화

위에서 의사결정 트리와 랜덤 포레스트로 검증을 진행하여 정확도를 변수에 각각 저장하였다.

이를 쉽게 알아보기 위해서 시각화를 하는 코드이다.

cv_list = [
    ['random_forest', rf_cv_scores],
    ['decision_tree', dt_cv_scores]
]

df = pd.DataFrame.from_dict(dict(cv_list))
df.plot()

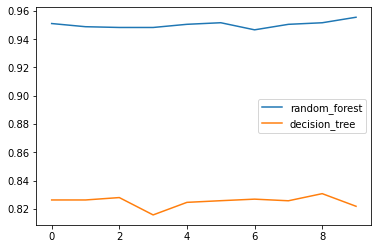
위의 그래프를 보면, 랜덤 포레스트의 성능이 의사결정 트리보다 월등히 높다는 것을 확인할 수 있다.

10회 진행한 정확도의 총 평균을 내면 다음과 같다.

# 의사결정 트리의 정확도 평균

np.mean(dt_cv_scores)

0.8252430167597765

# 랜덤 포레스트의 정확도 평균

np.mean(rf_cv_scores)

0.9502420856610799

　

　

예제2) 보팅 앙상블 손글씨 분류

이번 예제에서는 서로 다른 알고리즘의 모델들을 앙상블해서 손글씨 분류를 진행해보았다.

# 사용할 모듈 Import하기

from sklearn import datasets
from sklearn import tree
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

Data 불러오기

mnist = datasets.load_digits()
features = mnist.data
labels = mnist.target

X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size = 0.2)

　

　

단일 모델의 정확도 측정

앙상블 기법을 사용하기 전, 개별 모델(의사결정 트리, kNN, SVM)들 각각의 정확도를 측정해보았다.

동일한 조건에의서 정확도 비교를 위해서 모두 동일한 학습 Data를 사용하도록 하였다.

(random_state 변수를 동일하게 적용)

# 의사결정 트리 모델

dtree = tree.DecisionTreeClassifier(criterion = 'gini', max_depth = 8,
                                   max_features = 32, random_state = 35)
dtree = dtree.fit(X_train, y_train)
dtree_predicted = dtree.predict(X_test)


# kNN 모델

knn = KNeighborsClassifier(n_neighbors = 299).fit(X_train, y_train)
knn_predicted = knn.predict(X_test)


# SVM 모델

svm = SVC(C = 0.1, gamma = 0.003, probability = True, random_state = 35).fit(X_train, y_train)
svm_predicted = svm.predict(X_test)


# 정확도 출력

print('[ Accuracy ]')
print('d-tree : {}'.format(accuracy_score(y_test, dtree_predicted)))
print('knn : {}'.format(accuracy_score(y_test, knn_predicted)))
print('svm : {}'.format(accuracy_score(y_test, svm_predicted)))

[ Accuracy ]
d-tree : 0.7916666666666666
knn : 0.8416666666666667
svm : 0.9333333333333333

　

　

하드 보팅

‘scikit-learn’의 VotingClassifier() 함수를 이용하면 하드 보팅과 소프트 보팅을 구현할 수 있다.

따라서 이를 이용하여 하드 보팅과 소프트 보팅 모두 진행하였다.

voting_clf = VotingClassifier(estimators = [
    ('decision_tree', dtree), ('knn', knn), ('svm', svm)],
                             weights = [1, 1, 1], voting = 'hard').fit(X_train, y_train)

hard_voting_predicted = voting_clf.predict(X_test)
accuracy_score(y_test, hard_voting_predicted)

0.9194444444444444

　

　

소프트 보팅

voting_clf = VotingClassifier(estimators = [
    ('decision_tree', dtree), ('knn', knn), ('svm', svm)],
                             weights = [1, 1, 1], voting = 'soft').fit(X_train, y_train)

soft_voting_predicted = voting_clf.predict(X_test)
accuracy_score(y_test, soft_voting_predicted)

0.9083333333333333

　

　

단일 모델과 앙상블 모델의 정확도 비교 시각화

이렇게 해서 총 5개의 모델로 손글씨 분류를 진행해보았다.

5개의 개별 모델에 대한 정확도를 손쉽게 비교하기 위해서 bar 그래프를 그렸다.

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline


x = np.arange(5)

height_lists = [
    dtree_predicted,
    knn_predicted,
    svm_predicted,
    hard_voting_predicted,
    soft_voting_predicted
]

heights = []
for height_list in height_lists:
    heights.append(accuracy_score(y_test, height_list))

plt.bar(x, height = heights)
plt.xticks(x, ['decistion tree', 'knn', 'svm', 'hard voting', 'soft voting'])
plt.show()

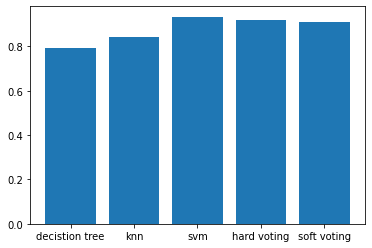
실행 결과, ‘SVM’ 모델이 가장 높은 정확도를 보여주는 것을 확인할 수 있다.

실행할 때마다 결과는 다르게 나올 수 있다. (처음에 진행했을 때는 ‘Soft Voting’ 모델에서 가장 높은 정확도가 나타났다.)

아무튼, 상황에 맞게 가장 좋은 성능이 좋은 모델을 선택하는 것이 중요하다!

　

　

마무리

이렇게해서 앙상블 기법에 대해서 알아보았다.

다음 포스트는 ‘비지도학습(Unsupervised Learning)’에 해당하는 ‘군집화(Clustering)’, 그 중에서 ‘k 평균 알고리즘(k-Means Clustering)’에 대해서 다룰 예정이다.

그럼, 다음 포스트에서 보도록 하겠다!