[Machine Learning] 선형회귀(Linear Regression)에 대해서 알아보기!

오늘 소개할 알고리즘은 선형회귀(Linear Regression)이다.

선형회귀는 지도학습(Supervised Learning) 중에서 대표적인 회귀분석 알고리즘이다.

이번에는 예제는 따로 없고, 랜덤으로 Data를 만들어서 선형회귀에 대한 실습만 진행하였다!

그럼, 일단 선형회귀에 대해서 이론을 알아보도록 하겠다.

　

　

이론

기존의 Data들을 기반으로 하나의 함수를 구해서 모르는 Data 값을 예측하는 알고리즘

　

사용되는 용어/개념 정리

회귀 계수(Regression Coefficient)

쉽게 말하면, 방정식의 계수이다.

$y = ax_1 + bx_2$

위의 1차 함수에서는 $a$와 $b$가 바로 회귀 계수이다.

　

선형 결합(Linear Combination)

서로 다른 벡터를 더해 새로운 벡터를 얻는 과정

바로 위에서 보았던

$y = ax_1 + bx_2$

이 함수에서도 $ax_1$과 $bx_2$를 각각 벡터로 가정한다면,

이 함수 역시 $x_1$이라는 벡터에 $a$라는 가중치를 곱한 벡터와 $x_2$라는 벡터에 $b$라는 가중치를 곱한 벡터의 선형 결합인 것이다.

　

평균 제곱 오차(Mean Squared Error, MSE)

각 Data와 함수 사이의 거리(error, 오차)를 제곱한 값을 모두 더해 평균낸 값

$y = \theta x$라는 함수가 있다고 해보자.

이때, $i$번째 Data와 이 함수의 오차는 다음과 같이 구할 수 있다.

$error = (y_i - \theta x_i)$

그렇다면, 제곱 오차(Squared Error)는 다음과 같다.

$square\;error = (y_i - \theta x_i)^2$

그냥 오차는 음수와 양수 모두를 값으로 가질 수 있지만, 제곱 오차는 항상 양수를 갖는다.

따라서 어느 회귀 모델이 나은지 비교할 때, 제곱 오차를 많이 사용한다.

이러한 방식으로 평균 제곱 오차(MSE)를 수식으로 나타내면 다음과 같다.

$f(\theta) = \frac{1}{n}\sum_{i=0}^n(y_i - \theta x_i)^2$

결국 선형회귀 모델의 목적 함수는 이 평균 제곱 오차 함수인 ‘$f(\theta)$’를 최소화하는 것이다!

　

경사 하강법(Gradient Descent)

회귀 계수를 구할 때 사용하는 방법 중 하나이다.

초기 회귀 계수를 임의값으로 설정한 후, 경사하강법을 반복해서 최소의 MSE를 가지는 회귀 계수($\theta$)를 구한다.

공식은 다음과 같다.

$\theta := \theta - \alpha \frac{\partial}{\partial\theta} f(\theta)$

여기서 $\alpha$는 ‘학습률(learning rate)’을 의미한다.

• $\alpha$의 값이 클수록 $\theta$의 값이 크게 변하며, $\alpha$의 값이 작을수록 $\theta$의 값이 작게 변한다.

공식을 설명하자면 이렇다!

어느 한 지점에서의 $f(\theta)$의 미분값과 반대되는 방향, 즉 -(미분값 x $\alpha$)만큼 $\theta$의 값을 변경해서 최적의 $\theta$의 값을 향해(변곡점에 더 가까운 값으로) 이동하는 것이다.

이 과정을 반복함으로써 $f(\theta)$를 최소로 하는 $\theta$값을 구하는 것이다.

　

　

실습) 선형회귀

위에서 이론에 대해서 설명하였으니, 이를 쉽게 이해하기 위해서 실습을 진행해보았다.

실습에서는 선형회귀(Linear Regression)에 대해서 시각적으로 이해하기 위해 $y = \omega x$의 형태를 갖는 선형회귀를 구현해보았다.

# 필요한 모듈 불러오기

from tensorflow.keras import optimizers
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

　

Data 생성 및 조회

실습에서 이용할 Data는 random모듈을 이용해서 랜덤으로 X와 Y Data를 생성하도록 하였다.

X = np.linspace(0, 10, 10)
Y = X + np.random.randn(*X.shape)

X값은 0부터 10사이에서 총 10개의 값을 랜덤하게 만들었다.

Y값은 생성된 X값에서 임의의 수를 더한 값으로 만들었다.

이때, X값에 더해지는 임의의 수는 ‘표준정규분포’에서 생성되는 난수이다.

for x, y in zip(X, Y):
    print((round(x, 1), round(y, 1)))
    # 출력할 때, 소수점 첫 째 자리에서 반올림하도록 했다.

(0.0, 0.7)
(1.1, 2.5)
(2.2, 3.1)
(3.3, 4.4)
(4.4, 5.3)
(5.6, 4.6)
(6.7, 7.4)
(7.8, 8.8)
(8.9, 9.4)
(10.0, 10.8)

X값과 Y값을 순서대로 출력해보았다.

총 10쌍의 Data가 잘 만들어진 것을 확인할 수 있다.

　

　

선형회귀 모델 만들기

tensorflow의 keras 모듈 중 Sequential()을 이용하여 선형회귀 모델을 구현하였다.

model = Sequential()  # 객체(모델) 생성
model.add(Dense(input_dim = 1, units = 1, activation = 'linear', use_bias = False))

Dense는 모델에 적용되는 Layer이다. Dense의 parameter에 대해서 설명하자면 다음과 같다.

• input_dim = 1 : 입력되는 $x$값이 하나이기 때문에 ‘1’로 설정
• units = 1 : 출력할 $y$값 또한 하나이기 때문에 ‘1’로 설정
• activation = 'linear' : 선형성을 유지하기 위함
• use_bias = False : 쉽게 말해서 $y = \omega x + b$를 가정하지 않아서 False로 설정함.

sgd = optimizers.SGD(learning_rate = 0.05)  # 경사하강법 optimizer 객체(모델) 생성
model.compile(optimizer = 'sgd', loss = 'mse')  # 훈련시킬 준비

$\omega$값을 최적화하기 위해서 경사하강법을 사용하였다.

따라서 sgd라는 변수에 경사하강법 optimizer 객체를 생성하였고, 이를 model에도 적용하였다.

weights = model.layers[0].get_weights()
w = weights[0][0][0]

print('initial w is : {}'.format(w))

initial w is : 0.43982231616973877

무작위로 설정된 초기 $\omega$값이다.

이제 아래에서 최적화된 $\omega$값을 찾을 것이다.

　

　

선형회귀 모델 학습

model.fit(X, Y, batch_size = 10, epochs = 10, verbose = 1)

Epoch 1/10
1/1 [==============================] - 0s 10ms/step - loss: 15.3328
Epoch 2/10
1/1 [==============================] - 0s 5ms/step - loss: 1.8800
Epoch 3/10
1/1 [==============================] - 0s 5ms/step - loss: 0.6990
Epoch 4/10
1/1 [==============================] - 0s 70ms/step - loss: 0.5953
Epoch 5/10
1/1 [==============================] - 0s 13ms/step - loss: 0.5862
Epoch 6/10
1/1 [==============================] - 0s 15ms/step - loss: 0.5854
Epoch 7/10
1/1 [==============================] - 0s 3ms/step - loss: 0.5853
Epoch 8/10
1/1 [==============================] - 0s 2ms/step - loss: 0.5853
Epoch 9/10
1/1 [==============================] - 0s 7ms/step - loss: 0.5853
Epoch 10/10
1/1 [==============================] - 0s 2ms/step - loss: 0.5853

model에 X, Y Data를 적용시켜 학습을 진행하였다.

출력된 학습 결과를 보면 알 수 있듯이, 학습을 하면 할수록 손실(loss)이 줄어들고 있다.

이는 MSE가 줄어들고 있다는 의미, 즉 최적의 $\theta$값을 찾아가고 있음을 의미한다.

또한 7번째 학습부터는 loss가 일정한 것으로 보아 7번째 학습에서 이미 최적의 $\theta$값을 찾았다고 볼 수 있다.

다음은 model.fit()의 parameter에 대한 설명이다.

• batch_size = 10 : 총 10개의 Data로 학습을 진행하였기 때문에 size를 10으로 지정하여 학습을 진행했다.
• epochs = 10 : 10번 반복 학습을 진행하도록 하였다.
• verbose = 1 : 학습 진행 상황을 출력할 수 있도록 하는 옵션이다. 0, 1, 2 등 총 3가지로 적용할 수 있으며, 숫자가 커질수록 더 자세하게 학습 진행 상황을 출력해준다.

　

　

모델 시각화

학습된 모델을 시각화하는 코드이다.

new_weights = model.layers[0].get_weights()
new_w = new_weights[0][0][0]  # 최적화된 w값을 새로 변수에 지정하였다.

plt.plot(X, Y, label = 'data')  # 실제 Data값을 연결한 그래프
plt.plot(X, new_w * X, label = 'prediction')  # 예측한 선형 회귀 그래프
plt.legend()
plt.show()

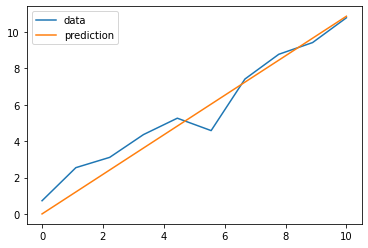
위의 그래프에서 볼 수 있듯이, 학습한 선형회귀 그래프가 실제값들과 근접하다는 것을 알 수 있다.

　

　

마무리

이렇게해서 선형회귀 알고리즘에 대해서 알아보았다.

관련된 실습만 있고, 예제가 없어서 좀 아쉬웠던 것 같다…

다음 포스트에서는 로지스틱 회귀(Logistic Regression)에 대해서 포스트할 예정이다.

근데 여태까지 했던 머신러닝 알고리즘 중에서 가장 내용이 복잡하고 많은 것 같다.

실습 예제도 종류가 상당히 많아 보이고…

아마 막막하다 싶으면 이론 정리는 건너뛸 수도 있을 것 같다…(얼핏 보니까 그럴 확률이 상당히 높아보임)

아무튼, 다음 포스트에서 보도록 하겠다!