[Machine Learning] 나이브 베이즈(Naive Bayes) 알고리즘을 활용해 붓꽃 분류하기!
오늘 소개할 알고리즘은 나이브 베이즈(Naive Bayes) 알고리즘이다.
그 중에서도 이번엔 가우시안 나이브 베이즈(Gaussian Naive Bayes) 알고리즘을 이용하여 붓꽃(iris)의 종류를 분류하는 예제를 실습해보았다!
그 외의 다항 분포 나이브 베이즈(Multinomial Naive Bayes), 베르누이 나이브 베이즈(Bernoulli Naive Bayes) 알고리즘에 대한 예제는 다음 포스트에서 다룰 예정이다.
일단 전체적인 나이브 베이즈 알고리즘에 대해서 설명해보도록 하겠다.
이론
Data를 단순(naive)하게 독립적인 사건으로 가정하고, 베이즈 이론에 대입시켜 가장 높은 확률의 레이블로 Data를 분류하는 알고리즘
즉, 이 알고리즘은 확률에 기반을 두고 있다!
사용되는 용어/개념 정리
나이브 베이즈 알고리즘에서 사용되는 개념과 용어들에 대해서 간단히 알아보도록 하자!
베이즈 이론 (Bayes’ Theorem)
$P(A \mid B) = \cfrac{P(B \mid A)P(A)}{P(B)}$
- $P(A \mid B)$ : 사건 B가 일어났을 때 사건 A가 일어날 확률
- $P(B \mid A)$ : 사건 A가 일어났을 때 사건 B가 일어날 확률
- $P(A), P(B)$ : 사건 A(B)가 일어날 확률
위의 A를 레이블, B를 데이터의 특징으로 대입하여 나이브 베이즈 알고리즘을 머신러닝에 응용한다.
$P(레이블 \mid 데이터 특징) = P(데이터 특징 \mid 레이블) x P(레이블) / P(데이터 특징)$
즉, 어떤 Data가 있을 때, 그에 해당하는 레이블은 기존 Data의 특징 및 레이블의 확률을 이용해 구할 수 있다!
근데 위는 Data의 특징이 1개일 때의 응용식이다.
Data의 특징이 늘어나면, 결합확률을 계산해야한다!
결합확률
$P(A, B) = P(A \mid B)P(B)$
하지만, 위에서도 언급했듯이, 나이브 베이즈 이론은 모든 사건을 독립 사건으로 가정하고 문제를 푼다고 했다!
모든 사건들이 독립일 때의 결합확률은 다음과 같이 계산한다.
$P(A, B) = P(A)P(B)$
특징이 여러 개인 경우의 나이브 베이즈 공식
n개의 특징을 가진 Data에 대한 나이브 베이즈 공식을 일반화하면 다음과 같다.
$P(y \mid x_1,…,x_n) = \cfrac{P(x_1 \mid y)P(x_2 \mid y)…P(x_n \mid y)P(y)}{P(x_1)P(x_2)…P(x_n)}$
나이브 가정을 통해서 모든 특징들을 독립적인 사건으로 계산하는 것이다.
여기서 곱을 나타내는 부분을 더 간단하게 줄이면,
$P(y \mid x_1,…,x_n) = \cfrac{P(y)\prod_{i=1}^n P(x_i \mid y)}{P(x_1)P(x_2)…P(x_n)}$
- $y$ : 레이블
- $x_n$ : Data의 n번째 특징
이러한 과정을 통해 구해지는 값들 중, 우리는 어떠한 레이블의 확률이 가장 큰 지만 알면 된다. 즉, 정확한 수치 값이 아닌 대소 비교만 할 수 있다면, 우리는 제일 큰 확률로 레이블을 분류할 수 있다.
나이브 베이즈 공식에서 분모는 ‘모든 특징들의 확률 곱’이며, 이는 모든 레이블이 공통적으로 가지는 분모이다.
따라서 대소 비교를 위해서는 이 부분을 계산할 때 생략해도 무방하다.
즉, 분자에 있는 값에 비례해서 레이블의 확률은 커지게 되고, 우리는 최종적으로 가장 높은 수치를 지닌 레이블로 Data를 분류하게 된다.
$y = argmax_y P(y)\prod_{i=1}^n P(x_i \mid y)$
여러가지 나이브 베이즈 모델
여러가지 나이브 베이즈 모델 중, 대표적인 3가지 정도를 소개하면 다음과 같다.
가우시안 나이브 베이즈 (Gaussian Naive Bayes)
가우시안 나이브 베이즈 모델은 Data 특징들의 값이 정규 분포(가우시안 분포)되어 있다는 가정하에 조건부 확률들을 계산한다.
따라서 이는 연속적인(continuous) 성질이 있는 특징을 가진 Data를 분류하는데 적합하다.
다항 분포 나이즈 베이즈 (Multinomial Naive Bayes)
다항 분포 나이브 베이즈 모델은 Data의 특징이 출현 횟수로 표현됐을 때 사용한다. (ex 주사위 던진 결과)
즉, 이는 이산적인(discrete) 성질이 있는 특징을 가진 Data를 분류하는데 적합하다.
베르누이 나이브 베이즈 (Bernoulli Naive Bayes)
베르누이 나이브 베이즈 모델은 Data의 특징이 0 또는 1로 표현됐을 때 사용한다.
즉, 이 또한 이산적인(discrete) 성질이 있는 특징을 가진 Data를 분류하는데 적합하다.
스무딩(smoothing)
학습 Data에 없던 Data가 출현해도 빈도수에 1을 더해서 확률이 0이 되는 현상을 방지하는 것
모델을 학습시킨 후 실제로 이용할 때, 학습 Data에는 없었던 Data가 실제 상황에서는 등장할 수 있다. 근데 학습된 모델은 이러한 Data의 확률을 0으로 계산하기 때문에 문제가 생긴다.
따라서 이러한 문제를 방지하고자 학습 Data에 없던 Data가 출현해도 빈도수에 1을 더해서 확률을 0으로 계산하지 않도록 하는 기술이 스무딩(smoothing)이다.
장/단점
장점
- 나이브 가정에 의해 모든 Data의 특징이 독립 사건이라고 가정했음에도 실제에서 높은 정확도를 보여줌.
- 나이브 가정 덕분에 계산 속도가 빠름.
단점
- 나이브 가정이 ‘문서 분류’에는 적합할지 몰라도 다른 분류 모델에서는 제약이 될 수 있음.
예제1) 가우시안 나이브 베이즈를 활용한 붓꽃 분류
Data 준비
# 필요한 모듈 Import하기
import pandas as pd
from sklearn.datasets import load_iris # 붓꽃 Data 로드
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn import metrics
from sklearn.metrics import accuracy_score
dataset = load_iris()
df = pd.DataFrame(dataset.data, columns = dataset.feature_names)
df['target'] = dataset.target
df.target = df.target.map({0:"setosa", 1:"versicolor", 2:"virginica"})
df.head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
DataFrame Columns 설명
- sepal length : 꽃받침 길이
- sepal width : 꽃받침 너비
- petal length : 꽃잎 길이
- petal width : 꽃잎 너비
- target : 붓꽃(irsi)의 종류(setosa, versicolor, virginica)
Data 시각화
iris Data가 어떻게 분포되어 있는지 시각화를 해보았다.
iris의 종류에 따라서 그래프를 그리기 위해 다음과 같이 DataFrame을 나누었다.
setosa_df = df[df.target == 'setosa']
versicolor_df = df[df.target == 'versicolor']
virginica_df = df[df.target == 'virginica']
ax = setosa_df['sepal length (cm)'].plot(kind = 'hist')
b = setosa_df['sepal length (cm)'].plot(kind = 'kde', ax = ax,
secondary_y = True,
title = 'setosa sepal lenght (cm) distribution',
figsize = (8, 4))
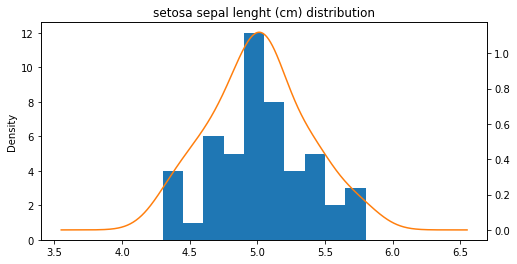
대표적으로 한 가지의 그래프를 보자면 위와 같다.
위는 ‘Setosa’의 꽃받침 길이 분포를 나타낸 그래프이다.
책에서는 그래프 하나만 코드를 대표적으로 보여주고, 나머지는 그림으로만 보여주었다.
하지만, 블로그에 나머지 그래프 그림도 보여주려면 결국 출력을 해야한다.
따라서 필요한 그래프를 한번에 그리는 함수 코드를 짜보았다.
코드는 다음과 같다.
# 그래프 한번에 그리는 함수를 만들어 봄.
import matplotlib.pyplot as plt
iris_df_list = [setosa_df, versicolor_df, virginica_df]
def plot_drawing_func(df_list):
i = 0
plt.figure(figsize = (30, 20))
for df in df_list:
name = df['target'].iloc[0]
columns_name = df.columns.tolist()[0:4]
for column in columns_name:
i += 1
plt.subplot(3, 4, i)
ax = df[str(column)].plot(kind = 'hist')
df[str(column)].plot(kind = 'kde', ax = ax,
secondary_y = True,
stacked = True,
title = '{0} {1} distribution'.format(name, column))
plot_drawing_func(iris_df_list)
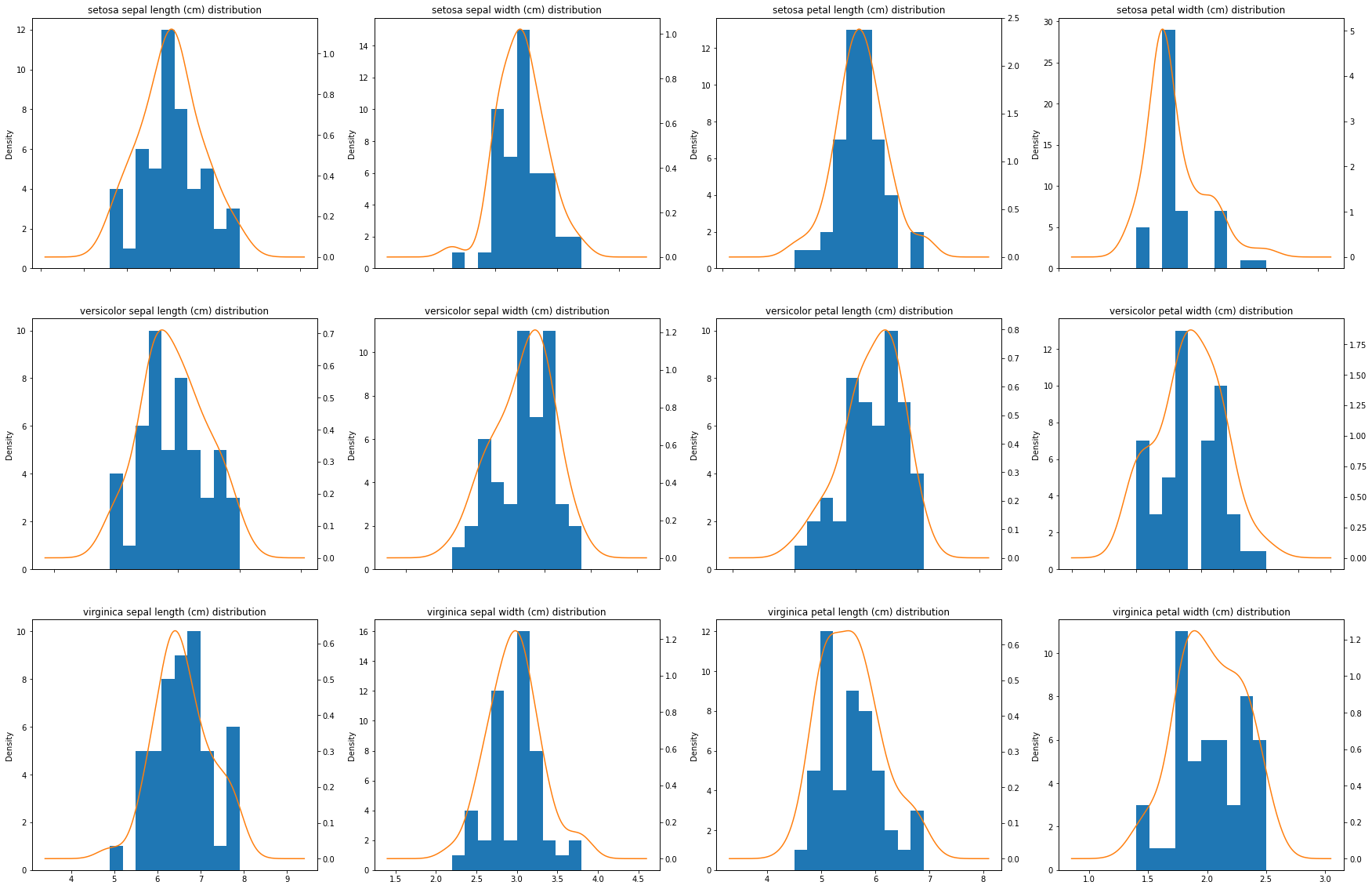
행(row) 맨 위부터 순서대로 ‘Setosa’, ‘Versicolor’, ‘Virginica’이고,
열(column) 맨 왼쪽부터 순서대로 ‘sepal length(꽃받침 길이)’, ‘speal width(꽃받침 너비)’, ‘petal length(꽃잎 길이)’, ‘petal width(꽃잎 너비)’이다.
그래프에서 볼 수 있듯이, Data의 모든 특징들이 정규분포에 가까운 분포를 가진다.
따라서 Data의 특징이 정규분포를 따른다는 가정하에 계산을 하는 ‘가우시안 나이브 베이즈 모델’로 에제를 진행했다.
Data 나누기
# 학습 Data, 테스트 Data 나누기
X_train, X_test, y_train, y_test = train_test_split(dataset.data, dataset.target, test_size = 0.2)
iris Data의 80%는 학습 Data, 20%는 테스트 Data로 나누었다.
모델 학습 및 테스트
Split한 Data를 바탕으로 가우시안 나이브 베이즈 모델을 학습 및 테스트 하였다.
model = GaussianNB()
model.fit(X_train, y_train)
expected = y_test
predicted = model.predict(X_test)
print(metrics.classification_report(expected, predicted))
print(accuracy_score(expected, predicted)) # 정확도
precision recall f1-score support
0 1.00 1.00 1.00 10
1 0.92 0.92 0.92 12
2 0.88 0.88 0.88 8
accuracy 0.93 30
macro avg 0.93 0.93 0.93 30
weighted avg 0.93 0.93 0.93 30
0.9333333333333333
모델 테스트 결과, 약 93%의 정확도를 보였다.
마무리
이로써 첫 번째 예제인 ‘가우시안 나이브 베이즈 모델을 통한 붓꽃(iris) 분류’를 마쳤다.
다음 포스트에서는 ‘베르누이 나이브 베이즈 모델을 활용한 스팸 메일 분류’, ‘다항분포 나이브 베이즈 모델을 활용한 영화 리뷰 분류’ 예제를 함께 다룰 예정이다.
나이브 베이즈 모델에 대한 예제가 많아서 나누어서 올리는 것이다.
그럼, 다음 포스트에서 보도록 하겠다!

댓글남기기