[Machine Learning] 주성분 분석(Principal Component Analysis)에 대해서 알아보기!
오늘 소개할 알고리즘은 주성분 분석(Principal Component Analysis)이다.
주성분 분석은 차원 축소 알고리즘 중 하나이다.
주성분 분석 알고리즘을 이해하는데는 선형대수의 지식이 상당히 필요한 것으로 보인다.
근데 2학년 1학기때 배운 선형대수는 기억이 나지 않는다…(교수님 죄송합니다)
일단, 주성분 분석 알고리즘에 대해 내가 이해한 바를 바탕으로 설명해보도록 하겠다!
이론
고차원의 Data를 저차원의 Data로 차원을 축소하는 알고리즘
위의 말 그대로 고차원의 Data를 저차원으로 차원을 축소해서 시각화 등에 사용할 수 있다.
단, 이때 Data의 고유한 특성을 최대한 유지하기 위해서 Data의 분산을 최대한 유지하는 것을 목적으로 한다.
예를 들어 x축, y축으로 이루어진 2차원에 Data들이 존재한다고 하자. 이 Data들은 1차원인 직선 상으로 차원을 축소할 수 있을 것이다.
이러한 경우에서 몇 가지를 생각해보도록 하자.
먼저, x축으로 차원을 옮기는 경우를 생각해보자.
만약 2차원 상에 y좌표는 다르지만 x좌표가 같은 Data가 있다면, 이는 x축으로 차원을 떨어뜨리면 중첩될 것이다.
즉 y좌표는 다르지만 x좌표가 비슷하거나 같다면 x축으로 차원을 떨어뜨렸을 때 Data들간에 중첩이 생겨 구분이 어려워질 것이다.
이는 y축으로 차원을 옮기는 경우에도 동일한 상황이 생길 수 있다!
하지만 x축, y축도 아닌 어떠한 1차원 직선상으로 모든 점들을 떨어뜨린다면 어떨까?
‘정사영’ 개념을 떠올리는 것이 가장 쉬울 것으로 생각된다.
Data들간의 중첩을 최소한으로 할 수 있는 직선을 찾을 수만 있다면 이는 2차원의 Data들의 특성을 최대한 유지해서 1차원으로 차원을 축소했다고 볼 수 있다.
주성분 분석(Principal Component Analysis, PCA) 알고리즘은 바로 그러한 라인을 찾아내는 알고리즘이다!
2차원이 아닌 더 높은 차원으로 올라가면 이러한 것을 구하기란 쉽지 않을 것이다.
여기서 수학적인 개념이 도입된다.
수학적으로 ‘Data의 중첩이 적다’라는 말은 ‘Data의 분산이 크다’라는 말과 동일하다.
따라서 주성분 분석 알고리즘은 분산이 가장 큰 차원을 선택해서 차원을 축소하게 된다.
그리고 분산이 가장 큰 차원은 공분산 행렬(Covariance Matrix)에서 고유값(Eigenvalue)이 가장 큰 고유벡터(Eigenvector)이다.
예를 들어 Data가 5차원이고 이를 2차원으로 차원을 축소하고 싶다고 가정해보자.
그렇다면 주성분 분석 알고리즘은 5차원 Data의 공분산 행렬에서 Eigenvalue가 큰 순서대로 나열한 후, 상위 2개의 Eigenvector를 축으로 2차원을 구성하여 Data의 차원을 축소하게 된다.
실습) 식습관 Data를 차원축소시켜서 시각화하기
이번 실습에서는 간단한 식습관 Data를 이용할 것이다.
이 Data들은 5개의 특징을 가진 5차원 Data이다.
이를 주성분 분석을 통해 1차원으로 차원을 축소해서 시각화하는 실습을 진행할 예정이다.
Data 생성
아래와 같이 총 6개의 Column을 가진 Dataframe을 생성하였다.
column 순서대로 ‘칼로리’, ‘아침’, ‘점심’, ‘저녁’, ‘운동 횟수’, ‘체형’을 의미한다.
import pandas as pd
df = pd.DataFrame(columns = ['calory', 'breakfast', 'lunch', 'dinner',
'exercise', 'body_shape'])
df.loc[0] = [1200, 1, 0, 0, 2, 'Skinny']
df.loc[1] = [2800, 1, 1, 1, 1, 'Normal']
df.loc[2] = [3500, 2, 2, 1, 0, 'Fat']
df.loc[3] = [1400, 0, 1, 0, 3, 'Skinny']
df.loc[4] = [5000, 2, 2, 2, 0, 'Fat']
df.loc[5] = [1300, 0, 0, 1, 2, 'Skinny']
df.loc[6] = [3000, 1, 0, 1, 1, 'Normal']
df.loc[7] = [4000, 2, 2, 2, 0, 'Fat']
df.loc[8] = [2600, 0, 2, 0, 0, 'Normal']
df.loc[9] = [3000, 1, 2, 1, 1, 'Fat']
df.head(10)
| calory | breakfast | lunch | dinner | exercise | body_shape | |
|---|---|---|---|---|---|---|
| 0 | 1200 | 1 | 0 | 0 | 2 | Skinny |
| 1 | 2800 | 1 | 1 | 1 | 1 | Normal |
| 2 | 3500 | 2 | 2 | 1 | 0 | Fat |
| 3 | 1400 | 0 | 1 | 0 | 3 | Skinny |
| 4 | 5000 | 2 | 2 | 2 | 0 | Fat |
| 5 | 1300 | 0 | 0 | 1 | 2 | Skinny |
| 6 | 3000 | 1 | 0 | 1 | 1 | Normal |
| 7 | 4000 | 2 | 2 | 2 | 0 | Fat |
| 8 | 2600 | 0 | 2 | 0 | 0 | Normal |
| 9 | 3000 | 1 | 2 | 1 | 1 | Fat |
Data 전처리
‘body_shape’ column을 제외한 나머지 Data 특징으로 ‘X’라는 Dataframe을 생성하였다.
그리고 ‘body_shape’ column은 ‘Y’라는 변수에 Dataframe으로 따로 저장하였다.
X = df[['calory', 'breakfast', 'lunch', 'dinner', 'exercise']]
Y = df[['body_shape']]
X.head()
| calory | breakfast | lunch | dinner | exercise | |
|---|---|---|---|---|---|
| 0 | 1200 | 1 | 0 | 0 | 2 |
| 1 | 2800 | 1 | 1 | 1 | 1 |
| 2 | 3500 | 2 | 2 | 1 | 0 |
| 3 | 1400 | 0 | 1 | 0 | 3 |
| 4 | 5000 | 2 | 2 | 2 | 0 |
Y.head()
| body_shape | |
|---|---|
| 0 | Skinny |
| 1 | Normal |
| 2 | Fat |
| 3 | Skinny |
| 4 | Fat |
Data 표준화
위의 Dataframe을 보면 현재 ‘calory’ column과 나머지 column 사이의 수치 범위가 너무나 큰 차이를 보인다.
이를 한 곳에 놓고 비교하기에는 좋지 않을 뿐더러 모델도 비교하는데 힘들어한다.
따라서 모든 Data들을 평균이 0이고 표준편차가 1인 Data로 표준화를 진행하였다.
from sklearn.preprocessing import StandardScaler
x_std = StandardScaler().fit_transform(X)
print(x_std)
[[-1.35205803 0. -1.3764944 -1.28571429 1. ]
[ 0.01711466 0. -0.22941573 0.14285714 0. ]
[ 0.61612771 1.29099445 0.91766294 0.14285714 -1. ]
[-1.18091145 -1.29099445 -0.22941573 -1.28571429 2. ]
[ 1.89972711 1.29099445 0.91766294 1.57142857 -1. ]
[-1.26648474 -1.29099445 -1.3764944 0.14285714 1. ]
[ 0.18826125 0. -1.3764944 0.14285714 0. ]
[ 1.04399418 1.29099445 0.91766294 1.57142857 -1. ]
[-0.15403193 -1.29099445 0.91766294 -1.28571429 -1. ]
[ 0.18826125 0. 0.91766294 0.14285714 0. ]]
공분산 행렬, 고유값, 고유벡터 구하기
먼저 각 5개 특징들의 공분산 행렬은 다음과 같다.
# 공분산 행렬 구하기
import numpy as np
features = x_std.T
covariance_matrix = np.cov(features)
print(covariance_matrix)
[[ 1.11111111 0.88379717 0.76782385 0.89376551 -0.93179808]
[ 0.88379717 1.11111111 0.49362406 0.81967902 -0.71721914]
[ 0.76782385 0.49362406 1.11111111 0.40056715 -0.76471911]
[ 0.89376551 0.81967902 0.40056715 1.11111111 -0.63492063]
[-0.93179808 -0.71721914 -0.76471911 -0.63492063 1.11111111]]
고유값(Eigenvalue)와 고유벡터(Eigenvector)는 다음과 같다.
# 고유값 및 고유벡터 구하기
eig_vals, eig_vecs = np.linalg.eig(covariance_matrix)
print('Eigenvectors \n{}\n'.format(eig_vecs))
print('Eigenvalues \n{}\n'.format(eig_vals))
Eigenvectors
[[-0.508005 -0.0169937 -0.84711404 0.11637853 0.10244985]
[-0.44660335 -0.36890361 0.12808055 -0.63112016 -0.49973822]
[-0.38377913 0.70804084 0.20681005 -0.40305226 0.38232213]
[-0.42845209 -0.53194699 0.3694462 0.22228235 0.58954327]
[ 0.46002038 -0.2816592 -0.29450345 -0.61341895 0.49601841]]
Eigenvalues
[4.0657343 0.8387565 0.07629538 0.27758568 0.2971837 ]
위에서 나온 Eigenvalue 중에서 그 값이 가장 큰 Eigenvector로 Data를 사영하여 Data의 차원을 축소하게 된다.
가장 첫 번째의 Eigenvalue가 가장 크므로 첫 번째에 해당하는 Eigenvector로 Data가 사영될 것이다.
eig_vals[0] / sum(eig_vals)
0.7318321731427544
위를 통해서 1차원으로 Data를 축소할 경우 원래 Data에서 약 73%에 해당하는 정보를 유지할 수 있다는 것을 알 수 있다.
즉, 27%의 정보는 손실된다는 것을 의미한다.
5차원 Data를 고유벡터로 사영시키기
A 벡터를 B 벡터로 사영하는 공식은 다음과 같다.
dot(A, B) / Magnitude(B)
(참고로 ‘Magnitude(B)’는 B벡터의 크기를 의미한다.)
따라서 코드로 이 수식을 구현하였다.
이번 실습에서 A 벡터는 ‘x_std’, B 벡터는 ‘eig_vecs’가 된다.
즉 원래의 Data(x_std)에서 고유벡터(Eigenvector)로 사영을 시켜서 차원을 축소하는 것이다.
Eigenvector로 사영시켜서 얻은 값들을 projected_X 변수에 원래 Data의 순서 그대로 저장하였다.
projected_X = x_std.dot(eig_vecs.T[0]) / np.linalg.norm(eig_vecs.T[0])
projected_X
array([ 2.22600943, 0.0181432 , -1.76296611, 2.73542407, -3.02711544,
2.14702579, 0.37142473, -2.59239883, 0.39347815, -0.50902498])
Data 시각화
최종적으로 가장 큰 값을 보여준 Eigenvalue에 해당하는 Eigenvector를 x축으로 하는 1차원에 Data들을 시각화하는 코드이다.
result = pd.DataFrame(projected_X, columns = ['PC1'])
result['y-axis'] = 0.0
result['label'] = Y
result.head(10)
| PC1 | y-axis | label | |
|---|---|---|---|
| 0 | 2.226009 | 0.0 | Skinny |
| 1 | 0.018143 | 0.0 | Normal |
| 2 | -1.762966 | 0.0 | Fat |
| 3 | 2.735424 | 0.0 | Skinny |
| 4 | -3.027115 | 0.0 | Fat |
| 5 | 2.147026 | 0.0 | Skinny |
| 6 | 0.371425 | 0.0 | Normal |
| 7 | -2.592399 | 0.0 | Fat |
| 8 | 0.393478 | 0.0 | Normal |
| 9 | -0.509025 | 0.0 | Fat |
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.lmplot('PC1', 'y-axis', data = result, fit_reg = False,
scatter_kws = {'s': 50}, hue = 'label')
plt.title('PCA result')
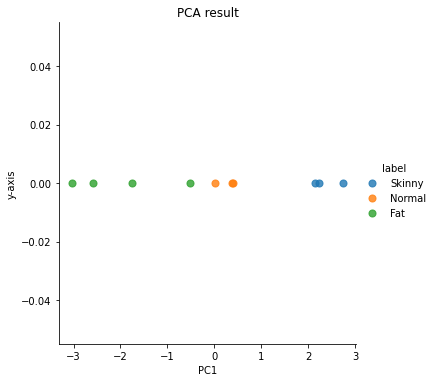
위의 그래프를 보면 각 레이블 별로 점의 색깔이 다른 것을 볼 수 있다.
같은 색깔의 점들이 모여있는 걸로 보아 Data의 특징이 잘 유지된 채로 차원 축소가 된 것을 확인할 수 있다.
scikit-learn을 활용해서 간단하게 구현하기
위에서는 수식을 직접 코드로 구현하여 주성분 알고리즘을 진행하였다.
하지만 사이킷런(scikit-learn)의 주성분 분석 라이브러리 모듈을 이용하면 쉽게 구현할 수 있다.
그 코드는 다음과 같다.
from sklearn import decomposition
pca = decomposition.PCA(n_components = 1)
sklearn_pca_x = pca.fit_transform(x_std)
sklearn_result = pd.DataFrame(sklearn_pca_x, columns = ['PC1'])
sklearn_result['y-axis'] = 0
sklearn_result['label'] = Y
sns.lmplot('PC1', 'y-axis', data = sklearn_result, fit_reg = False,
scatter_kws = {'s': 50}, hue = 'label')
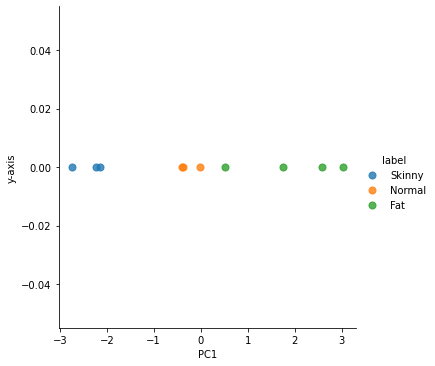
이전의 그래프와 비교해보면 점의 위치가 반대로 되어있다.
점의 위치를 제외하면 모든 것이 동일하다.
확인해보니 공분산 행렬, Eigenvalue 등의 값들은 모두 동일하게 나오는데 Eigenvector의 부호만 반대로 나온다.
따라서 projected_X의 부호도 반대로 나와서 그런지 그래프에서도 점의 위치가 반대로 나왔다.
커널을 재시작해서 다시 실행시켜봐도 동일하게 나와서 뭐가 문젠지는 모르겠지만… 아무튼 그렇다.
책 저자분이 깃허브에 올려주신 노트북을 실행해봐도 이상하게 반대로 나온다. 뭐가 문제일까…
아무튼, 점의 위치만 반대로 나오는 것을 제외하면 문제가 없어 보인다!
마무리
주성분 분석 알고리즘에 대해서 알아보다 보니 정태수 교수님의 말씀이 떠올랐다.
‘경영공학개론’ 기말고사가 끝나고 마지막 수업 때 교수님이 선형대수를 잘 알아놓으라고 하셨다.
그 이유가 무엇인지 알 수 있었던 것 같다.
Eigenvalue, Eigenvector… 이런 것들을 선형대수 수업때 배운 것은 기억이 나는데
계산을 어떻게 했고, 이런 것들이 기억이 나질 않는다…
이번 학기에 듣고 있는 군학점 수업 ‘데이터학습과지능’에서도 선형대수가 나올 것으로 보인다.
아무래도 선형대수에 대해서도 간단히 복습하면서 공부를 해야될 것 같다!!
이번 포스트를 마지막으로 머신러닝에 대한 알고리즘은 모두 끝났다! 물론, 책에서 소개하는 알고리즘이 끝난 것이다.
책에서는 다음 Chapter부터 딥러닝에 대한 개념과 알고리즘을 소개한다.
따라서 다음 포스트부터는 딥러닝에 대한 내용을 포스팅할 것 같다.
어떻게 진행될 지는 모르겠지만, 다음 포스트에서 보도록 하겠다!

댓글남기기