[Machine Learning] k-평균 알고리즘(k-Means Clustering)을 활용해 키-몸무게에 따른 체형 군집화하기!
오늘 소개할 알고리즘은 k-평균 알고리즘(k-Means Clustering)이다.
k-평균 알고리즘은 대표적인 비지도학습(Unsupervised Learning) 알고리즘인 군집화(Clustering) 중 하나이다.
이번 예제는 놀랍도록 간단해서 실망적…
Data Set이 너무나 지나치도록 간단하다…
k-평균 알고리즘에 대한 이론 설명을 보기 좋게 이해할 수 있도록 도와주는 간단한 예제인 듯하다!
더 큰 Data Set으로도 한번 돌려보고 싶다.
그럼, k-평균 알고리즘에 대해서 알아보도록 하겠다.
이론
Data간의 거리를 사용해 가까운 거리에 있는 Data끼리 클래스로 묶으면서 분류하는 알고리즘
k-평균 알고리즘(k-Means Clustering)은 Data간의 거리를 사용해서 Data들을 분류하기 때문에 수치화된 Data를 필요로한다.
k-평균 알고리즘은 다음의 단계를 거치면서 진행된다.
1. k값 정하기 - 몇 개의 군집(Cluster)으로 분류할 것인가
‘k-평균 알고리즘’에서의 ‘k’는 몇 개의 군집(Cluster)으로 Data들을 분류할 것인가를 나타내는 변수이다.
__이 k값은 사용자가 정의하는 하이퍼파라미터(Hyperparameter)__이다.
2. 군집(Cluster)의 최초 중심(Centroid) 설정
‘k’값을 정의했으면, 다음은 각각의 클러스터의 중심(Centroid)을 설정해야한다. Cluster의 수만큼 설정된 Centroid를 기준으로, Centroid와 Data 간의 거리를 비교하여 가장 가까운 Centroid의 Cluster로 분류하게 된다.
기본적으로 k-평균 알고리즘에서는 최초 Centroid를 무작위로 설정한다. 하지만, 상황에 따라선 최초 Centroid를 사용자가 먼저 설정할 수도 있다.
또한 scikit-learn의 KMeans 라이브러리의 ‘kmean++’라는 알고리즘을 적용할 수도 있다. 이 ‘kmean++’ 알고리즘은 k-평균 알고리즘에서 기본적으로 채택하는 랜덤 Centroid 설정 방식을 보완하기 위해서 만들어진 알고리즘이다. 이 알고리즘에 대한 설명은 생략하도록 하겠다.
3. Data를 가장 가까운 군집(Cluster)으로 설정
2번에서 설명했던 것처럼, 랜덤으로 Centroid가 설정되었다면 이제 각각의 Centroid와 Data 간의 거리를 계산해서 제일 가까운 Centroid가 포함된 Cluster로 Data를 소속시키게 된다.
이 과정을 모든 Data들에 대해 적용하면, 모든 Data들은 각각 어느 한 Cluster에 소속을 가지게 된다.
4. 중심(Centroid)을 군집(Cluster)에 속한 Data들의 가운데 위치로 변경
3번 단계가 완료되면, 각각의 Cluster에 해당하는 Centroid의 위치를 변경한다.
그 위치는 각각의 Cluster에 속한 Data들의 가운데이다.
5. 중심(Centroid)가 바뀌지 않을 때까지 3, 4번 단계 반복
4번 단계에서 Centroid의 위치가 바뀌면, 그 바뀐 Centroid를 기준으로 다시 Data간의 거리를 계산해서 Data들을 어느 한 Cluster에 소속시킨다.
어떤 Data는 이전과 같은 Cluster에 속하게 될 것이고, 또 어떤 Data는 바뀐 후의 다른 Centroid와 더 가까워서 이전과 다른 Cluster에 속하게 될 수도 있다.
이 과정을 각각의 Centroid의 위치가 바뀌지 않을 때까지 계속해서 반복한다.
Centroid가 더 이상 바뀌지 않으면, k-평균 알고리즘에 의해서 Data의 분류가 완료된 것이다.
예제) 키와 몸무게에 따른 체형 군집화
말로만 설명해서 이해가 안됐을 수도 있으니, 간단한 Data를 이용하여 예제를 보면서 설명하겠다!
# 필요한 모듈 불러오기
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
Data 만들기 및 시각화
일단 군집화(Clustering)에 이용할 Data를 만들어주었다.
df = pd.DataFrame(columns = ['height', 'weight'])
data_list = [
[185,60],
[180,60],
[185,70],
[165,63],
[155,68],
[170,75],
[175,80]
]
for i in range(len(data_list)):
df.loc[i] = data_list[i]
df
| height | weight | |
|---|---|---|
| 0 | 185 | 60 |
| 1 | 180 | 60 |
| 2 | 185 | 70 |
| 3 | 165 | 63 |
| 4 | 155 | 68 |
| 5 | 170 | 75 |
| 6 | 175 | 80 |
여담이지만, 책의 코드는 df의 자료들을 그냥 노가다 식으로 할당했다.
df.loc[0] = [185,60]
df.loc[1] = [180,60]
뭐 이런 식으로 말이다.
근데 보자마자 그냥 비효율적이다(?)라는 생각과 함께 for문을 이용하면 될 것 같아서 나름대로 코드를 바꿔보았다.
물론 쓰고 보니 원래 책의 코드보다 길어지긴 했지만…ㅎㅎㅎ
아무튼 이 Dataframe을 시각화하면 다음과 같다.
sns.lmplot('height', 'weight',
data = df, fit_reg = False,
scatter_kws = {'s': 200})
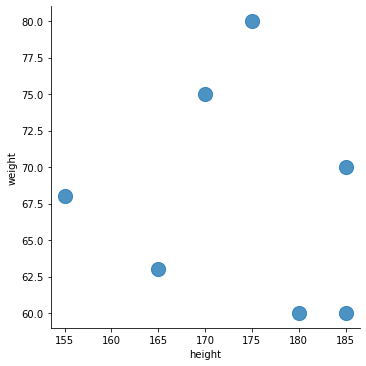
k-평균 알고리즘 시각화
위에서 만든 Data를 바탕으로 k-평균 알고리즘을 통해 군집화를 해보면 다음과 같다.
data_points = df.values
kmeans = KMeans(n_clusters = 3).fit(data_points)
# 'n_clusters'가 바로 k값(하이퍼파라미터)를 지정하는 변수이다.
df['cluster_id'] = kmeans.labels_
sns.lmplot('height', 'weight', data = df, fit_reg = False,
scatter_kws = {'s': 150}, hue = 'cluster_id')
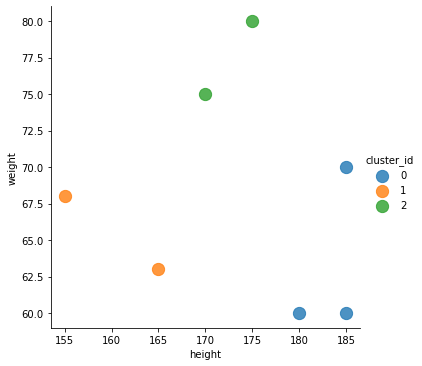
위의 그래프에서 같은 색의 점으로 나타나는 것은 같은 군집(Cluster)로 분류된 것이다.
그래프를 보면, 비슷한 Data끼리 군집화가 잘 된 것을 확인할 수 있다.
마무리
이렇게해서 군집화 중 k-평균 알고리즘에 대해서 알아보았다.
예제가 너무 초간단해서 좀 아쉽긴 하지만… 나중에 혼자서라도 더 큰 Dataset으로 실습을 해봐야겠다.
다음 포스트에서는 ‘선형회귀(Linear Regression)’에 대해서 포스트할 예정이다.
그럼, 다음 포스트에서 보도록 하겠다!

댓글남기기