[Machine Learning] k-최근접 이웃(kNN) 알고리즘으로 농구선수 포지션 예측하기!

이전 포스트에서 소개한 머신러닝 책에서 처음으로 소개하는 머신러닝 알고리즘이 바로,

k-최근접 이웃 (k-Nearest Neighbor, kNN) 알고리즘이다.

이는 대표적인 지도학습(Supervised Learning) 알고리즘으로, 데이터 분류(Classification)에 이용된다.

책에서는 이 알고리즘과 2017년 NBA 농구선수의 실제 게임 Data를 이용해 농구선수의 포지션을 예측하는 예제를 진행했다.

이번 포스트에서는 나 나름대로 예제를 하면서 정리한 내용을 포스팅할 예정이다.

Jupyter Notebook에 과정을 진행해가면서 정리하고 싶은 것들을 주석달면서 진행해봤다.

~~그리고나서 md파일로 그대로 다운받아고 블로그에 업로드해서 그런지 약간 어색할 수도 있음~~

이론

기존의 Data 안에서 현재 Data로부터 가까운 k개의 Data를 찾아 k개의 레이블 중 가장 많이 분류된 값으로 현재의 Data를 분류하는 알고리즘

이때 ‘k’는 몇 개의 가까운 Data를 찾을 것인지를 나타내는 변수 (홀수로 지정하는 것이 좋다! 과반수의 결과를 얻기 위함!)

‘k’에 따라서 결국 Data가 다르게 예측되는 것인데, 그 최적의 ‘k’값을 찾는 것이 중요!

그럴려면 검증을 통해서 가장 정확도가 높은 ‘k’를 찾아서 사용해야한다.

즉, 거리를 측정해서 가까운 Data를 찾는 것인데, 이때 머신러닝에서는 벡터 공간을 사용한다.

이중 분류는 2차원 벡터 공간을, 다중 분류에서는 n차원 벡터 공간을 사용함.
다중 분류의 경우, 4차원 이상이면 시각화는 힘들지만 알고리즘 상에서는 문제 없음!
우리가 흔히 알고있는 ‘피타고라스의 방식’으로 Data 간의 거리를 구하게 된다.
2차원이 아니어도 거리를 구하는 방식은 n차원으로 늘어나도 동일하기 때문에 거리 계산은 가능하다.

장/단점

장점

거리를 구하는 방식을 사용 -> 즉, 숫자로 된 Data에 사용하면 높은 정확도를 기대할 수 있음.
예측 시점에서 Data가 주어지면 바로 기존 Data와의 거리를 계산하기 때문에 미리 모델 학습을 할 필요가 없음. -> 실시간 Data 사용에 유리
이러한 특성을 게으른 학습(Lazy Learning)이라고 함!

단점

한 가지의 Data를 예측할 때, 모든 Data와의 거리를 계산 -> 속도가 느리고, 메모리 사용 多
예측 값이 주변 정보에 의해서 많이 편향될 가능성 있음(미리 학습된 모델이 아니라 가까운 이웃 Data로만 예측하기 때문)

예제) 농구선수의 게임 데이터를 활용한 포지션 예측

Data 살펴보기

import pandas as pd

df = pd.read_csv('DS060/data/csv/basketball_stat.csv')
df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 100 entries, 0 to 99
Data columns (total 8 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   Player  100 non-null    object 
 1   Pos     100 non-null    object 
 2   3P      100 non-null    float64
 3   2P      100 non-null    float64
 4   TRB     100 non-null    float64
 5   AST     100 non-null    float64
 6   STL     100 non-null    float64
 7   BLK     100 non-null    float64
dtypes: float64(6), object(2)
memory usage: 6.4+ KB

df.head()

	Player	Pos	3P	2P	TRB	AST	STL	BLK
0	Alex Abrines	SG	1.4	0.6	1.3	0.6	0.5	0.1
1	Steven Adams	C	0.0	4.7	7.7	1.1	1.1	1.0
2	Alexis Ajinca	C	0.0	2.3	4.5	0.3	0.5	0.6
3	Chris Andersen	C	0.0	0.8	2.6	0.4	0.4	0.6
4	Will Barton	SG	1.5	3.5	4.3	3.4	0.8	0.5

df.value_counts('Pos')

Pos
SG    50
C     50
dtype: int64

이쯤에서 사용하는 Data에 대한 간략한 설명을 하자면(책에 있는 표를 그대로 인용하여 설명하자면),

약어	설명
Player	선수 이름
Pos	포지션
3P	한 경기 평균 3점슛 성공 횟수
2P	한 경기 평균 2점슛 성공 횟수
TRB	한 경기 평균 리바운드 성공 횟수
AST	한 경기 평균 어시스트 성공 횟수
STL	한 경기 평균 스틸 성공 횟수
BLK	한 경기 평균 블로킹 성공 횟수

포지션 설명 ~~이후의 과정을 설명하려면 필요해서…~~

C : 센터; 블로킹, 리바운드 역할, 공을 바깥으로 빼서 공격 찬스를 만들기도 하고, 골대 근처에서 2점슛으로 득점도 함.
SG : 슈팅가드; 3점슛 등 장거리에서 슛을 해서 점수를 얻는 역할을 함.

두 포지션을 구분할 수 있는 속성으로 ‘블로킹’, ‘리바운드’, ‘3점슛’을 선정.

하지만, 이렇게 구분할 수 있는 속성을 고른 건 그저 가설일 뿐이니까 가설의 사실을 입증해야 함. -> 데이터 시각화가 좋은 수단 중 하나!

따라서 각각의 변수에 대해 관계를 알아보기 위해서 간단한 산점도를 그려보았다.

import matplotlib.pyplot as plt
import seaborn as sns  # Matplotlib을 기반으로 하고 다양한 기능을 추가한 시각화 패키지 
%matplotlib inline
# Notebook 안에서 코드 실행 결과(그림)을 볼 수 있도록 해주는 매직 커맨드


sns.lmplot('STL', '2P', data = df, fit_reg = False, # True인 경우 추세선이 그려짐
          scatter_kws = {'s':150}, # 좌표 상의 점 크기 조절
          markers = ['o', 'x'],
          hue = 'Pos') # 점을 찍고 싶은 변수 (예측값)

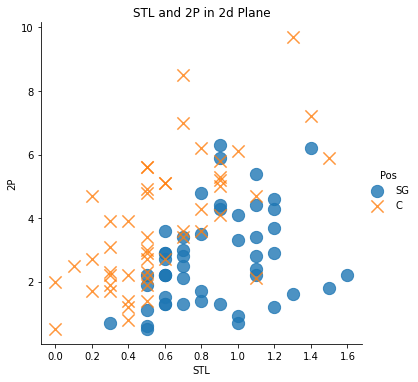
plt.title('STL and 2P in 2d Plane')

png

import matplotlib.pyplot as plt
import seaborn as sns  # Matplotlib을 기반으로 하고 다양한 기능을 추가한 시각화 패키지 
%matplotlib inline
# Notebook 안에서 코드 실행 결과(그림)을 볼 수 있도록 해주는 매직 커맨드


sns.lmplot('AST', '2P', data = df, fit_reg = False, # True인 경우 추세선이 그려짐
          scatter_kws = {'s':150}, # 좌표 상의 점 크기 조절
          markers = ['o', 'x'],
          hue = 'Pos') # 점을 찍고 싶은 변수 (예측값)

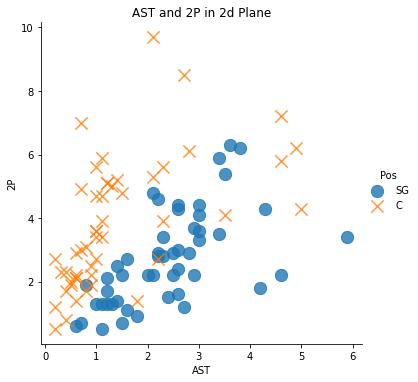
plt.title('AST and 2P in 2d Plane')

png

import matplotlib.pyplot as plt
import seaborn as sns  # Matplotlib을 기반으로 하고 다양한 기능을 추가한 시각화 패키지 
%matplotlib inline
# Notebook 안에서 코드 실행 결과(그림)을 볼 수 있도록 해주는 매직 커맨드


sns.lmplot('BLK', '3P', data = df, fit_reg = False, # True인 경우 추세선이 그려짐
          scatter_kws = {'s':150}, # 좌표 상의 점 크기 조절
          markers = ['o', 'x'],
          hue = 'Pos') # 점을 찍고 싶은 변수 (예측값)

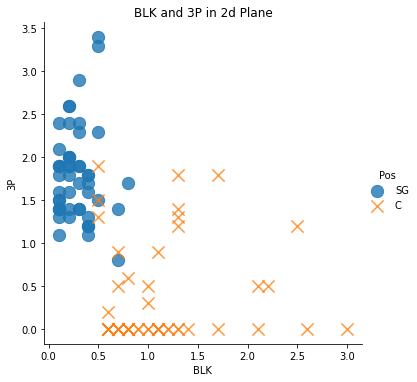
plt.title('BLK and 3P in 2d Plane')

png

import matplotlib.pyplot as plt
import seaborn as sns  # Matplotlib을 기반으로 하고 다양한 기능을 추가한 시각화 패키지 
%matplotlib inline
# Notebook 안에서 코드 실행 결과(그림)을 볼 수 있도록 해주는 매직 커맨드


sns.lmplot('TRB', '3P', data = df, fit_reg = False, # True인 경우 추세선이 그려짐
          scatter_kws = {'s':150}, # 좌표 상의 점 크기 조절
          markers = ['o', 'x'],
          hue = 'Pos') # 점을 찍고 싶은 변수 (예측값)

plt.title('TRB and 3P in 2d Plane')

png

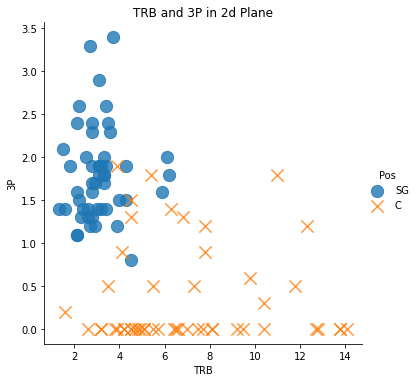
4가지 그래프 모두를 보면 알 수 있듯이, Data의 구분이 확실하지 않음(경계가 너무 근접해서 분류하기 모호) -> 가설이 타당해보임!

Data 다듬기

분류하는데 도움이 되지 않는 특징(‘2점슛(2P)’, ‘어시스트(AST)’, ‘스틸(STL)’)은 제거(drop()함수를 이용)

df.drop(['2P', 'AST', 'STL'], axis = 1, inplace = True)
# 'inplace = True' : 함수 실행 후 반환되는 객체를 바로 df로 사용하겠다는 의미
# default 값은 'inplace = False'

df.head()

	Player	Pos	3P	TRB	BLK
0	Alex Abrines	SG	1.4	1.3	0.1
1	Steven Adams	C	0.0	7.7	1.0
2	Alexis Ajinca	C	0.0	4.5	0.6
3	Chris Andersen	C	0.0	2.6	0.6
4	Will Barton	SG	1.5	4.3	0.5

Data 나누기

사이킷런의 train_test_split()을 이용하여 학습 Data와 테스트 Data로 분리.

from sklearn.model_selection import train_test_split

train, test = train_test_split(df, test_size = 0.2)  # 테스트 Data의 비율이 20%가 되도록 설정

# 'test_size = 0.2' = 'train_size = 0.8'

type(train)  # split한 Data의 type은 Pandas의 DataFrame

pandas.core.frame.DataFrame

train.info()  # 80개의 Data

<class 'pandas.core.frame.DataFrame'>
Int64Index: 80 entries, 9 to 92
Data columns (total 5 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   Player  80 non-null     object 
 1   Pos     80 non-null     object 
 2   3P      80 non-null     float64
 3   TRB     80 non-null     float64
 4   BLK     80 non-null     float64
dtypes: float64(3), object(2)
memory usage: 3.8+ KB

test.info()  # 20개의 Data

<class 'pandas.core.frame.DataFrame'>
Int64Index: 20 entries, 81 to 95
Data columns (total 5 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   Player  20 non-null     object 
 1   Pos     20 non-null     object 
 2   3P      20 non-null     float64
 3   TRB     20 non-null     float64
 4   BLK     20 non-null     float64
dtypes: float64(3), object(2)
memory usage: 960.0+ bytes

train 변수에는 train Data가, test 변수에는 test Data가 원래의 df에서 각각 80%, 20%의 비율로 나누어졌음.

최적의 ‘k’값 찾기

방법은 여러가지가 있음!

train_test_split()을 이용해 Data 나눔 -> (검증 Data의 레이블) vs (kNN 알고리즘 모델 예측값) 비교
사이킷런의 cross_val_score()을 이용 (책에서는 이 방법을 이용함.)

cross_val_score()을 이용하면 쉽게 kNN 모델의 교차 검증을 수행할 수 있음!

이때 교차 검증은 ‘k-fold 교차 검증’!

‘k-fold’ 교차 검증이란,

기존 Data를 k개로 나누고, k개로 나눠진 Data를 모두 검증 Data로 한 번씩 사용함. 이렇게 k번 검증을 하고 이때의 정확도들을 평균내는 방식.

다음은 ‘k-fold 교차 검증’을 위한 코드이다.

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score


max_k_range = train.shape[0] // 2
k_list = []
for i in range(3, max_k_range, 2):
    k_list.append(i)
    
cross_validation_scores = []
x_train = train[['3P', 'BLK', 'TRB']]
y_train = train[['Pos']]


for k in k_list:
    knn = KNeighborsClassifier(n_neighbors = k)
    scores = cross_val_score(knn, x_train, y_train.values.ravel(), cv = 10, scoring = 'accuracy')
    cross_validation_scores.append(scores.mean())
    
cross_validation_scores

[0.875,
8875,
9125,
925,
9,
9,
9125,
8875,
8875,
875,
875,
8625,
8375,
8125,
8125,
8125,
8125,
8125,
8]

# k에 따른 정확도를 그래프로 시각화

plt.plot(k_list, cross_validation_scores)
plt.xlabel('the number of k')
plt.ylabel('Accuracy')
plt.show()

png

위의 그래프를 보면 k값이 9일 때, 정확도가 가장 높다는 것을 알 수 있다.

k = k_list[cross_validation_scores.index(max(cross_validation_scores))]
print('The best number of k : {}'.format(k))

The best number of k : 9

모델 테스트

모델 테스트를 진행하기 위한 코드는 다음과 같다.

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

knn = KNeighborsClassifier(n_neighbors = k)  # 위에서 구한 최적의 'k'값이 지정됨

x_train = train[['3P', 'BLK', 'TRB']]
y_train = train[['Pos']]

knn.fit(x_train, y_train.values.ravel())  # kNN 모델 학습

x_test = test[['3P', 'BLK', 'TRB']]
y_test = test[['Pos']]

pred = knn.predict(x_test)  # 테스트 시작 -> 결과를 'pred' 변수에 저장 (array type)

print('accuracy : {}'.format(accuracy_score(y_test.values.ravel(), pred)))

accuracy : 0.9

comparison = pd.DataFrame({'prediction':pred, 'ground_truth':y_test.values.ravel()})
comparison

# 'prediction'은 예측값, 'ground_truth'는 실제값

	prediction	ground_truth
0	SG	SG
1	SG	SG
2	C	C
3	SG	C
4	SG	SG
5	SG	SG
6	C	C
7	C	C
8	SG	SG
9	C	C
10	SG	SG
11	C	C
12	SG	SG
13	C	C
14	C	C
15	SG	SG
16	C	C
17	C	SG
18	C	C
19	C	C

‘k’값이나, 정확도(accuracy)나 코드를 실행할 때마다 다르게 측정된다.

랜덤으로 테스트 Data와 훈련 Data가 나누어지다 보니 그런 것 같다.

마무리

처음으로 머신러닝 알고리즘을 접해보게 되었다. 저자분께서도 말씀했듯이, 어려운 지식 없이 쉽게 이해할 수 있는 알고리즘이라서 괜찮았던 것 같다.

다음은 ‘서포트 벡터 머신(SVM)’이다.

또 공부하고 정리해서 다음 포스트로 찾아오도록 하겠다!

Twitter Facebook LinkedIn

Jihoon, Jeong

[Machine Learning] k-최근접 이웃(kNN) 알고리즘으로 농구선수 포지션 예측하기!

이론

장/단점

장점

단점

예제) 농구선수의 게임 데이터를 활용한 포지션 예측

Data 살펴보기

Data 다듬기

Data 나누기

최적의 ‘k’값 찾기

모델 테스트

마무리

공유하기

댓글남기기

참고

[Deep Learning] 난관에 봉착했다…!

[Deep Learning] 퍼셉트론(Perceptron)으로 AND/OR 연산 구현하기!

[Machine Learning] 주성분 분석(Principal Component Analysis)에 대해서 알아보기!

[Machine Learning] 로지스틱 회귀(Logistic Regression)에 대해서 알아보기!

	prediction	ground_truth
0	SG	SG
1	SG	SG
2	C	C
3	SG	C
4	SG	SG
5	SG	SG
6	C	C
7	C	C
8	SG	SG
9	C	C
10	SG	SG
11	C	C
12	SG	SG
13	C	C
14	C	C
15	SG	SG
16	C	C
17	C	SG
18	C	C
19	C	C

	prediction	ground_truth
0	SG	SG
1	SG	SG
2	C	C
3	SG	C
4	SG	SG
5	SG	SG
6	C	C
7	C	C
8	SG	SG
9	C	C
10	SG	SG
11	C	C
12	SG	SG
13	C	C
14	C	C
15	SG	SG
16	C	C
17	C	SG
18	C	C
19	C	C

	prediction	ground_truth
0	SG	SG
1	SG	SG
2	C	C
3	SG	C
4	SG	SG
5	SG	SG
6	C	C
7	C	C
8	SG	SG
9	C	C
10	SG	SG
11	C	C
12	SG	SG
13	C	C
14	C	C
15	SG	SG
16	C	C
17	C	SG
18	C	C
19	C	C